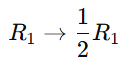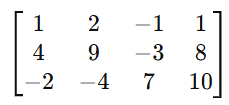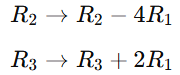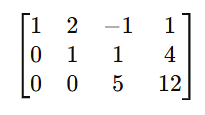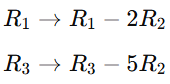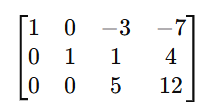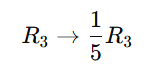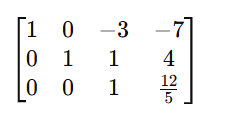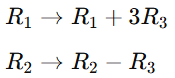Cramer’s rule 2×2 , 3×3 is a method used to solve systems of linear equations using determinants. So It applies to systems of n linear equations with n variables, assuming that the determinent of the co-efficient matrix is non zero. This rule provides precise formulas for solving a system of linear equations using determinants.
Consider this system of linear equations:

where:
- A is a square matrix (with size n×n)
- x is a column vector of unknowns x_1,x_2,…,x_ n,
- b represents a column vector of constants. b_1,b_2,…,b_n
The matrix equation can be written as:

Step-by-Step Instructions for Cramer’s rule 2×2
1. Calculate the determinant of the coefficient matrix: Check if matrix A’s determinant (det(𝐴)) is non-zero. Because if det(A) = 0, the system lacks a unique solution and cannot be solved using Cramer’s Rule.
2. Construct Matrices A_1, A_2,…, A_n: For each unknown x_i, construct a new matrix A_i by substituting the i-th column of matrix A with the column vector b. Substitute the constants from vector b for the i-th column of A to produce the i-th matrix A_i.
- A1 is formed by replacing the first column of A with b
- A2 is created by substituting b for A’s second column.
- and so on for all columns.
3. Calculate the determinants of the modified matrix: Determine the determinant of each matrix A i, denoted as det(A_i), for each i=1, 2,…,n.
4. Solve for Each x_i: The solution for each unknown x_i is given by:

for i=1,2,…,n.
For example:
Consider this system of linear equations:

The coefficient matrix A is:

The column vector b is

Step 1: Firstly, Calculate det(A)

Step 2: Create matrices A_1 and A_2.
- For x, replace the first column of A with b:

- For y, change the second column of A to b:

Step 3: Compute the determinants of A_1 and A_2


then,
Step 4: Solve for x and y:


So, lastly, the solution to the system is:

Cramer’s rule 2×2 simplifies the process of solving linear equations using determinants. However, it is computationally expensive for big systems due to the necessity to calculate numerous determinants.
Practice problems
1.

2.

3.

4.


 algebra4 months ago
algebra4 months ago
 algebra4 months ago
algebra4 months ago
 geometry4 months ago
geometry4 months ago
 algebra5 months ago
algebra5 months ago
 algebra4 months ago
algebra4 months ago
 algebra5 months ago
algebra5 months ago
 calculus5 months ago
calculus5 months ago
 geometry3 months ago
geometry3 months ago