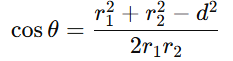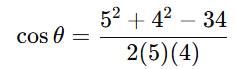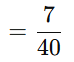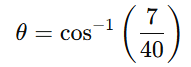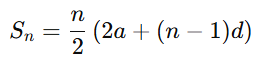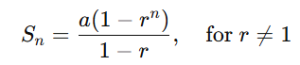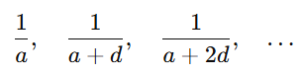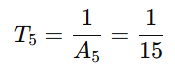All formulas of circle
All formulas of circle are essential concepts in geometry.
Definition
A circle is the set of all points in a plane that are equidistant from a fixed point called the center. The distance from the center to any point on the circle is called the radius (r).
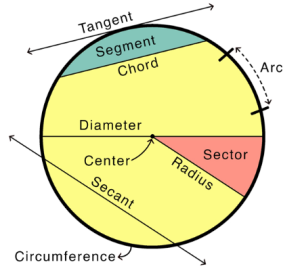
Here
- Diameter: The diameter is twice the radius: D = 2r.
- Circumference: The circumference (C) is the total distance around the circle: C=2πr
- Area: The area enclosed by the circle is
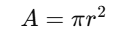
- Chord: A chord is a line segment joining two points in the circle.
- Arc: An arc is a part of the circle’s circumference.
- Sector: A sector is a region enclosed by two radii and an arc.
Standard equation of a circle
The equation of circle depends on its center and radius
(a) Circle centered at the origin (0,0)
If the center is at the origin and the radius is r, then the equation is:
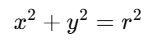
(b) Circle centered at (h,k)
If the center is at (h, k), and the radius is r, the equation is :
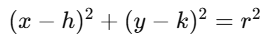
General equation of a circle
The expanded form of a circle’s equation is :
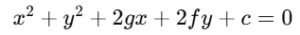
- The center is given by (-g,-f).
- The radius is
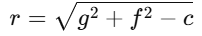
Important properties of circle
1. Tangents and normals to a circle
A tangent is a line that touches the circle at exactly one point.The tangent to the circle equation
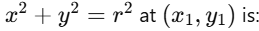
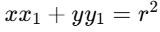
In a general equation, x^2 +y^2 +2gx+2fy+c=0 , the equation of the tangent at (x_1,y_1) is:
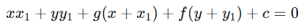
2. Polar form of a circle: In polar coordinates (r,θ), the equation of a circle centered at the origin is
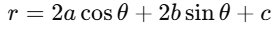
3. Position of any points with respect to a circle:
Distance formula: Calculate the distance d of the point (x_1,y_1) from the center (h,k):
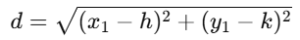
Now, compare d with the radius r:
- If d<r: The point is inside the circle.
- If d=r : The point is on the circle.
- If d>r : The point is outside the circle.
4. Length of tangent from the point (x_1, y_1) to the circle: The length of the tangent from an external point (x_1, y_1) to a circle with equation
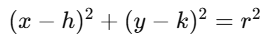
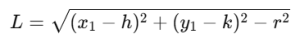
Example
Given circle
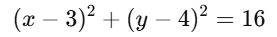
Find the tangent length from (7,1)
Using the formula
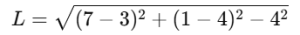
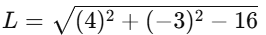

5. Angle of Intersection of two circles
The angle of intersections between two circles refers to the angle between their tangents at the points of intersection.It can be calculated using the formula
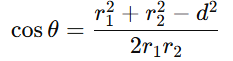
Example
Given two circles
(x-2)^2+(y-3)^2=25 – Center(2,3), Radius r_1=5
(x-7)^2+(y-6)^2=16 -Center(7,6), Radius r_2=4
Step 1: Find distance between centers
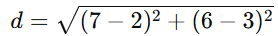
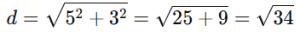
Step 2: Apply the formula
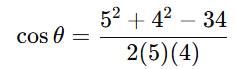
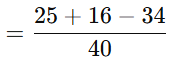
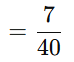
Step 3: Find θ
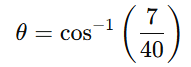
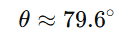
Special cases
1. Orthogonal circles ( θ=90∘)
- Two circles are orthogonal (intersect at right angles) if their centers and radii satisfy
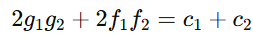
- This means cosθ=0 and θ=90∘
2. Concentric circles
- If two circles share the same center (d = 0), they do not intersect or are the same circle .
3. Circles touching externally (θ=0∘)
- If d=r1+r2, then they touch externally.
4. Circles touching internally (θ=180∘)
- If d=∣r1−r2∣ they touch internally.
These are All formulas of circle.


 algebra4 months ago
algebra4 months ago
 algebra4 months ago
algebra4 months ago
 geometry4 months ago
geometry4 months ago
 algebra5 months ago
algebra5 months ago
 algebra4 months ago
algebra4 months ago
 algebra5 months ago
algebra5 months ago
 calculus5 months ago
calculus5 months ago
 geometry3 months ago
geometry3 months ago

 (both numerator and denominator approach 0)
(both numerator and denominator approach 0) (both numerator and denominator approach ∞)
(both numerator and denominator approach ∞)

 which is an indeterminate form
which is an indeterminate form