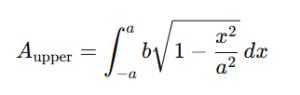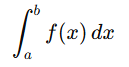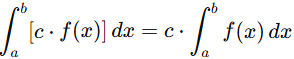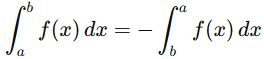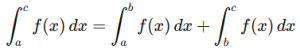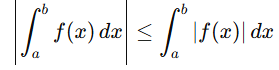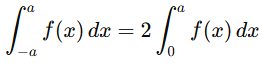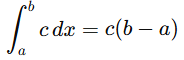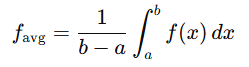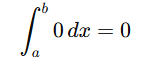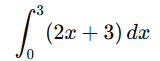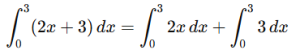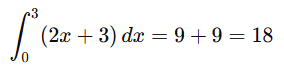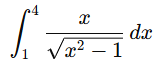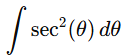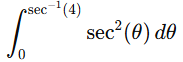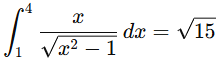Definite integral properties: Linearity , Reversal of limits, Zero width, Additivity, Bounds Inclusion, Comparison property, Absolute Value, Even and odd functions, Integration of a constant, Average value of a function, Additivity with zero contribution.
What is a definite integral?
A definite integral is a mathematical process that estimates the accumulation of quantities over an interval of time. The mathematical expression is as follows:
Here, and are the integration limits, is the function under consideration and represents an infinitesimally small change in. This process produces a number, which is commonly used to represent an area, volume, or other accumulated value.
Mathematical Representation
The definite integral of a function f(x) over the interval [a,b] is written as:
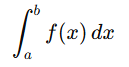
Here
- a: The lower limit of integration.
- b: The upper limit of integration.
- f(x): The function to be integrated.
- dx represents an infinitesimal change in x.
The Geometric interpretation
One of the simplest and most straightforward ways to understand definite integrals is through geometric interpretation. Consider a curve defined by on a graph. The definite integral from to calculates the net area between the curve and the -axis over the interval.
- Area above the x-axis: Contributions from add to the total.
- Area above the y-axis: contributions from subtracting from the total.
Properties of definite integrals
1. Linearity: Definite integral respects the principles of addition and scalar multiplication.
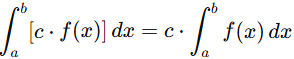
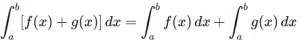
This means you can split the integral across sums or factor out constants.
2. Reversal of limits : Reversing the order of the limits of integration modifies the sign of the integral.
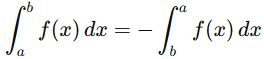
3. Zero width: The outcome is 0 if the integral’s upper and lower limits are equal.
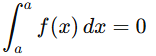
This is because no area is accumulated over a zero-width interval.
4. Additivity (splitting intervals): A definite integral over an interval can be split into subintervals.
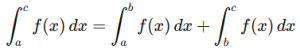
This is useful for breaking complex integrals into manageable parts.
5. Bounds Inclusion: If f(x) is continuous on [a,b], then:
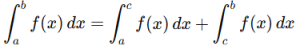
This property is often used to handle piecewise functions.
6. Comparison property: If f(x) ≤ g(x) for any x in [a,b], then:
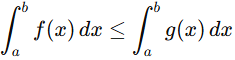
If the functions are strictly ordered, the inequality becomes strict.

7. Absolute Value: The absolute value of an integral does not equal the integral of the absolute value in general.
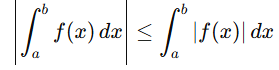
This inequality reflects that the definite integral accounts for signed areas.
8. Even and odd functions
- For an even function F(x)=F(-x) , integrated over symmetric limits
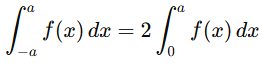
- For an odd function F(x)=-F(-x), integrated over symmetric limits
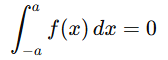
9. Integration of a constant: If f(x) = c , where c is a constant, then:
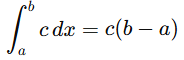
This is the area of a rectangle whose width is b−a and its height is c.
10. Average value of a function: The definite integral can be used to compute the average value of f(x) over [a,b]
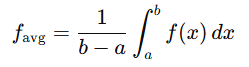
11. Additivity with zero contribution: If f(x)=0 over an interval, then:
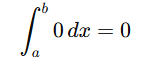
These are Definite integral properties.
Example 1:
Evaluate
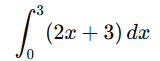
Using linearity:
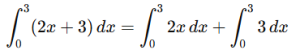
Compute each term
S0
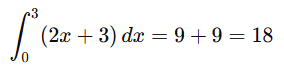
Example 2:
Evaluate
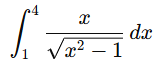
Step 1: Analyze the problem
The integrand 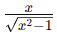 suggests that a substitution related to the square root
suggests that a substitution related to the square root 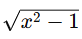 will simplify the integral . Let’s proceed with a trigonometric substitution.
will simplify the integral . Let’s proceed with a trigonometric substitution.
Step 2: Sustitution
Let,
x=Sec(θ) , dx=Sec(θ) tan(θ) dθ
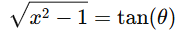
The integral becomes
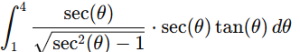
Simplify
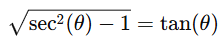
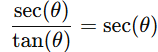
Thus the integrand simplifies to
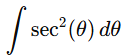
Step 3: Adjust limits of integration
When x=1 :
x= sec(θ) ⟹sec(θ)=1 ⟹θ=0
when x=4
x= sec(θ) ⟹sec(θ)=4 ⟹θ=sec−1(4)
The new limits are
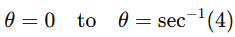
Step 4: Integrate
The integral is now
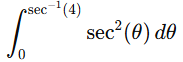
The antiderivative of sec^2(θ) is tan(θ).
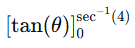
Step 5: Evaluate
Substitute the limits
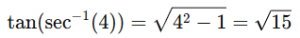
and at θ=0 tan(0)=0
Thus
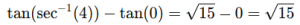
Final Answer
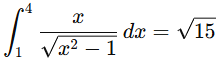
Learn more indefinite integral

 algebra4 months ago
algebra4 months ago
 algebra4 months ago
algebra4 months ago
 geometry4 months ago
geometry4 months ago
 algebra5 months ago
algebra5 months ago
 algebra5 months ago
algebra5 months ago
 algebra5 months ago
algebra5 months ago
 calculus5 months ago
calculus5 months ago
 geometry3 months ago
geometry3 months ago