Trigonometric Rules is a fundamental discipline of mathematics that studies the relationships between the sides and angles of triangles, specifically right-angled triangles. These relationships are expressed using different trigonometric ratios and identities.
1. Trigonometric ratios
In a right triangle, there are six primary trigonometric ratios that relate the angles of the triangle to the lengths of its sides. Let’s define the sides of a right triangle:
- Hypotenuse: The longest side opposite the right angle.
- Adjacent: The side next to the angle of interest (not the hypotenuse).
- Opposite: The side opposite the angle of interest.
The six trigonometric ratios are:






These ratios are essential tools for solving problems involving angles and lengths in right triangles.
2. Pythagorean identities
These identities come from the Pythagorean theorem, which asserts that in a right-angled triangle:

From this, we can deduce the following fundamental identities:
First Identity:

Second Identity:

Third Identity:
 These identities are extremely helpful in simplifying expressions involving trigonometric functions.
These identities are extremely helpful in simplifying expressions involving trigonometric functions.
3. Angle sum and Difference Formulas
These formulas express the trigonometric functions of the sum or difference of two angles as a function of the individual angles.
Sine:


Cosine:


Tangent:


These formulas are critical for simplifying trigonometric expressions, particularly when dealing with angles in addition and subtraction problems.
4. Formulas for Double Angles
When the angle of a Trigonometric Rules doubles, double angle formulae are utilized. From the sum formulas, these formulas can be obtained.


Alternatively, you can express it as:

Or


Expressions with a double angle can be made simpler with the help of these formulas.
5. Half-Angle Formulas



6. For any triangle, the Law of Sines

8. For any triangle, the Law of Cosines

9. Product-to-sum identity for sine and cosine




10. Sum of Angles in a Triangle:
In any triangle, the sum of the angles is 180∘ or π


 algebra1 month ago
algebra1 month ago
 algebra1 month ago
algebra1 month ago
 algebra2 months ago
algebra2 months ago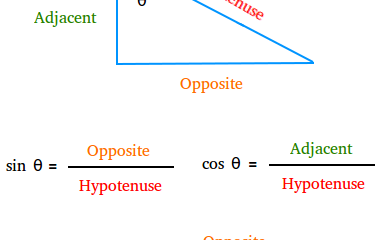
 algebra1 month ago
algebra1 month ago
 geometry1 month ago
geometry1 month ago
 calculus2 months ago
calculus2 months ago
 algebra2 months ago
algebra2 months ago
 algebra2 months ago
algebra2 months ago